기저함수
기저함수는 선형대수학에서 매우 중요한 개념 중 하나이다. 기저함수란 임의의 함수를 다른 함수들의 선형조합으로 표현하는데 사용되는 함수들을 의미한다. 즉, 기저함수는 일종의 벡터공간 안에서 서로 다른 어떤 함수들을 표현하기 위해 사용되는 기초적인 함수들이라고 할 수 있다.
기저함수는 기저 벡터와 비슷한 역할을 한다. 기저 벡터는 벡터공간 안에서 어떤 벡터를 다른 벡터들의 선형조합으로 표현하는데 사용되는 벡터들을 의미한다. 기저함수 역시 벡터공간 안에서 어떤 함수를 다른 함수들의 선형조합으로 표현하는데 사용되는 함수들을 의미한다.
기저함수의 역할과 중요성
기저함수는 다양한 영역에서 매우 중요한 역할을 한다. 예를 들어, 기저함수는 신호처리에서 매우 중요하게 사용된다. 신호를 다른 함수들의 선형조합으로 표현하는데 사용되는 기저함수는 이러한 신호처리에서 매우 중요한 역할을 한다.
기저함수는 선형대수학에서 매우 중요한 개념으로, 많은 문제들을 해결하는데 필수적이다. 기저함수는 다양한 수학적인 분야에서 활용되며, 실제 세계에서 발생하는 많은 문제들을 해결하는데도 매우 중요한 역할을 한다.
기저함수의 종류와 특징
기저함수는 다양한 종류가 있으며, 각각의 종류는 특징이 다르다. 기저함수의 종류를 알아보면서, 각각의 특징을 살펴보자.
1. 표준 기저함수
표준 기저함수는 가장 일반적으로 사용되는 기저함수 중 하나이다. 표준 기저함수는 임의의 x값에 대해 0이 아니고, 다른 x값에 대해 0인 함수들로 이루어져 있다. 표준 기저함수는 다항식 함수들인 x, x^2, x^3, … 이나 삼각함수들인 sin(x), cos(x) 등이 있다.
2. 기저 생성함수
기저 생성함수는 어떤 벡터공간을 이루는 벡터들을 만드는데 사용되는 함수들을 의미한다. 기저 생성함수는 일정한 조건을 만족하는 벡터들의 집합을 생성하는데 사용할 수 있다. 예를 들어, 일차독립의 벡터들로 이루어진 벡터공간에서는 이러한 생성함수들이 유용하게 사용된다.
3. 행렬 기저함수
행렬 기저함수는 벡터공간에서 사용되는 함수들로, 벡터공간 안의 벡터들을 행렬로 표현한 후 이를 연산하는 함수들을 의미한다. 행렬 기저함수는 고유값과 고유벡터를 구하는데 매우 유용하게 사용된다.
기저함수의 사용 예시와 응용
기저함수는 수치해석, 미분방정식, 신호처리, 통계학, 물리학, 공학 등 수많은 분야에서 사용된다. 이러한 분야에서 기저함수가 사용되는 몇 가지 예시를 살펴보자.
1. 신호처리
신호처리에서는 신호를 다른 함수들의 선형조합으로 표현하는데 사용되는 기저함수가 매우 중요하게 사용된다. 이러한 기저함수는 신호처리에서 필수적이며, 이를 통해 다양한 분석과 변환을 수행할 수 있다.
2. 물리학
물리학에서는 기저함수가 다양한 분야에서 사용된다. 예를 들어, 양자역학에서는 파동함수를 다른 파동함수들의 선형조합으로 표현하는데 기저함수가 사용된다.
3. 통계학
통계학에서는 다양한 분포함수들이 기저함수를 사용하여 표현된다. 예를 들어, 정규분포의 밀도함수는 가우시안 함수들의 선형조합으로 표현된다.
4. 미분방정식
미분방정식에서는 기저함수가 초기값 문제를 해결하는데 사용된다. 초기값 문제란, 미분방정식에서 초기조건이 주어졌을 때, 해를 구하는 문제를 의미한다.
기저함수를 이용한 신호의 선형 변환
기저함수를 이용한 신호의 선형변환은 다양한 신호처리에서 매우 중요하게 사용된다. 신호를 이용한 선형변환은 텐서와 비슷한 개념으로, 신호에서 요소를 추출하거나 신호에 변화를 줄 수 있다.
기저함수를 이용한 선형변환은 매우 유용하며, 다양한 신호처리에서 사용되는 필수적인 기술이다.
기저함수와 푸리에 변환의 관계
기저함수와 푸리에 변환은 매우 밀접한 관계가 있다. 푸리에 변환은 신호를 주파수 성분으로 분해하는데 사용되는데, 이때 기저함수로는 코사인 함수와 사인 함수가 사용된다.
즉, 푸리에 변환은 정현파와 부정현파로 구성된 함수들을, 코사인 함수와 사인 함수들의 선형조합으로 표현한다. 이러한 기저함수를 이용하여 신호를 분해할 수 있으며, 이를 이용하여 신호처리를 수행할 수 있다.
기저함수와 최소 자승법의 관계
기저함수와 최소자승법은 매우 밀접한 관계가 있다. 최소자승법은 어떤 데이터를 가장 잘 설명하는 함수를 찾는데 사용되는데, 이때 기저함수를 사용할 수 있다.
최소자승법에서는 잔차의 합을 최소화할 수 있는 함수를 찾는데, 기저함수는 이를 구하는데 사용될 수 있다. 이러한 방식으로, 최소자승법을 이용하여 데이터를 해석하면서 기저함수를 사용할 수 있다.
기저함수의 선택 방법 및 최적화
기저함수의 선택 방법은 매우 중요하다. 기저함수의 선택은 데이터 해석에 큰 영향을 미치며, 특정 기저함수를 선택하지 않으면 원하는 결과를 얻을 수 없다.
기저함수의 선택은 데이터 자료와 문제 해결에 따라 다르며, 최적화 알고리즘이 필요하다. 최적화 알고리즘은 기저함수의 선택을 최적화하며, 이를 이용하여 데이터 해석을 수행한다.
FAQs
Q1. 기저함수의 정의는 무엇인가?
A: 기저함수는 벡터공간 안에서 어떤 함수를 다른 함수들의 선형조합으로 표현하는데 사용되는 기초적인 함수들이다.
Q2. 기저함수는 어떤 분야에서 사용되는가?
A: 기저함수는 수치해석, 미분방정식, 신호처리, 통계학, 물리학, 공학 등 수많은 분야에서 사용된다.
Q3. 기저함수의 종류는 무엇이 있는가?
A: 기저함수의 종류로는 표준 기저함수, 기저 생성함수, 행렬 기저함수 등이 있다.
Q4. 기저함수를 이용한 신호의 선형변환은 무엇인가?
A: 기저함수를 이용한 신호의 선형변환은 신호에서 요소를 추출하거나 신호에 변화를 줄 수 있는 기술이다.
Q5. 기저함수와 푸리에 변환의 관계는 무엇인가?
A: 기저함수와 푸리에 변환은 매우 밀접한 관계가 있다. 푸리에 변환은 신호를 주파수 성분으로 분해하는데 사용되는데, 이때 기저함수로는 코사인 함수와 사인 함수가 사용된다.
Q6. 기저함수의 선택 방법은 어떻게 이루어지는가?
A: 기저함수의 선택은 데이터 자료와 문제 해결에 따라 다르며, 최적화 알고리즘이 필요하다. 최적화 알고리즘은 기저함수의 선택을 최적화하며, 이를 이용하여 데이터 해석을 수행한다.
사용자가 검색한 키워드: 기저함수 Basis function, 기저 벡터란, 기저 판별, 표준기저, 기저 정리, 기저 의미, 행렬 기저, 기저 생성
Categories: Top 59 기저함수
기저의 개념 (basis)
여기에서 자세히 보기: shinbroadband.com
Basis function
In this article, we will focus on basis functions in the context of the Korean language. Korean is a unique language with complex grammar rules and varying sentence structures. Understanding the basis functions of the Korean language can help with tasks such as machine translation, text-to-speech synthesis, and language modeling.
Basis Functions in Grammar
In the study of language, grammar is the set of rules that governs the structure of sentences. Basis functions play a crucial role in describing the structure of sentences in any language, including Korean.
In Korean, the basic sentence structure is subject-object-verb (SOV). For example, the sentence “I ate breakfast” in English would be translated to “나는 아침을 먹었다” in Korean, where “나는” (na-neun) is the subject, “아침을” (a-chim-eul) is the object, and “먹었다” (meog-eoss-da) is the verb.
There are several basis functions that can be used to describe the structure of Korean sentences. These functions include:
– Subject marker (이/가)
– Object marker (을/를)
– Topic marker (은/는)
– Contrastive topic marker (은/는)
The subject marker (이/가) is used to indicate the subject of a sentence. In the example sentence above, “나는” (na-neun) is the subject, and the marker “는” (neun) is used to indicate this.
The object marker (을/를) is used to indicate the direct object of a sentence. In the example sentence above, “아침을” (a-chim-eul) is the direct object, and the marker “을” (eul) is used to indicate this.
The topic marker (은/는) is used to indicate the topic of a sentence. In Korean, the topic of a sentence is often placed at the beginning of the sentence, before the subject. For example, “아침을 먹었다” (a-chim-eul meog-eoss-da) could be rewritten as “아침은 먹었다” (a-chim-eun meog-eoss-da) if the topic of the sentence is breakfast.
The contrastive topic marker (은/는) is used to indicate a contrast or comparison between different topics. For example, “나는 밥을 먹고, 친구는 영화를 봤다” (na-neun bap-eul meog-go, chin-gu-neun yeong-hwa-reul bwat-da) means “I ate rice, and my friend watched a movie”. The contrastive topic marker “는” (neun) is used to compare the different topics, in this case, the activities of the speaker and their friend.
Basis Functions in Machine Translation
Machine translation is the task of automatically translating text from one language to another. Basis functions play a crucial role in this task, as they provide a structured representation of the grammar and syntax of a language.
In machine translation, one common approach is to use a neural machine translation (NMT) system. These systems use artificial neural networks to learn the translation patterns between two languages. Basis functions can be used to encode the structure of the source language and the target language into the neural network.
For example, consider the sentence “나는 한국어를 공부하고 있어요” (na-neun han-guk-eo-reul gong-bu-ha-go iss-eo-yo), which means “I am studying Korean”. In an NMT system, this sentence would be encoded using basis functions such as the subject marker, object marker, and verb tense markers. These basis functions provide a structured representation of the grammar and syntax of the sentence, which can be used to translate it into another language.
Basis Functions in Text-to-Speech Synthesis
Text-to-speech (TTS) synthesis is the task of automatically generating speech from written text. Basis functions play a crucial role in this task, as they provide a structured representation of the phonetics and prosody of a language.
In TTS synthesis, one common approach is to use a concatenative synthesis method. This method involves combining pre-recorded speech units (such as phonemes or diphones) to generate new speech. Basis functions can be used to align the pre-recorded speech units to the written text, and to adjust their timing and pitch to match the prosody of the language.
For example, consider the sentence “안녕하세요” (an-nyeong-ha-se-yo), which means “hello” in Korean. In TTS synthesis, this sentence would be encoded using basis functions such as the vowel and consonant phonemes, and the prosodic markers such as the pitch and stress. These basis functions provide a structured representation of the phonetics and prosody of the sentence, which can be used to generate a natural-sounding speech.
Basis Functions in Language Modeling
Language modeling is the task of predicting the probability of a sequence of words in a language. Basis functions play a crucial role in this task, as they provide a structured representation of the grammar and syntax of the language.
In language modeling, one common approach is to use a recurrent neural network (RNN) or a transformer network. These networks use basis functions such as word embeddings, part-of-speech tags, and syntactic parses to learn the patterns of the language. Basis functions can be also used to represent the context of the sentence and paragraph, which is crucial for natural language understanding tasks.
For example, consider the sentence “한국에서 여행한 적이 있나요?” (han-guk-e-seo yeo-haeng-han jeok-i iss-na-yo?), which means “Have you ever traveled to Korea?” In language modeling, this sentence would be encoded using basis functions such as the subject and object markers, the question marker (이/가 아니라), and the past tense marker (-았/었). These basis functions provide a structured representation of the grammar and syntax of the sentence, which can be used to predict the probability of a sequence of words in the language.
FAQs
Q: What are basis functions?
A: Basis functions are a set of functions that can be linearly combined to estimate the shape of a data set. They are commonly used in statistics and mathematical modeling.
Q: What are basis functions in the Korean language?
A: In the Korean language, basis functions are used to describe the structure of sentences and the phonetics and prosody of the language. They include functions such as the subject marker, object marker, topic marker, and contrastive topic marker.
Q: How are basis functions used in machine translation?
A: In machine translation, basis functions provide a structured representation of the grammar and syntax of the source and target languages. They are used to encode sentences into a neural network, which can learn the translation patterns between the languages.
Q: How are basis functions used in text-to-speech synthesis?
A: In text-to-speech synthesis, basis functions provide a structured representation of the phonetics and prosody of the language. They are used to align pre-recorded speech units to written text, and to adjust their timing and pitch to match the prosody of the language.
Q: How are basis functions used in language modeling?
A: In language modeling, basis functions provide a structured representation of the grammar and syntax of the language. They are used to represent the context of the sentence and paragraph, which is crucial for natural language understanding tasks.
기저 벡터란
기저 벡터란 벡터 공간의 기초를 이루는 선형 독립적인 벡터들을 말합니다. 이를테면, x-y 평면이라고 해보겠습니다. 그렇다면, 우리는 2개의 기저 벡터, 즉 (1,0)과 (0,1)을 가질 수 있습니다. 이 벡터들은 위에서 언급한 것과 같이 선형 독립적이고, x-y 평면의 모든 다른 벡터들은 이 기저 벡터들의 선형 조합으로 표현될 수 있습니다.
기저 벡터는 그들을 선형 조합하여 얻을 수 있는 다른 벡터들의 가장 작은 집합입니다. 그들은 꼭 벡터 공간의 차원 수와 같은 수의 벡터가 필요합니다.
기저 벡터는 어떻게 선택되나요?
기저 벡터를 선택하는 법에는 여러 가지가 있습니다. 일반적으로는 일반적으로 가장 간단한 선택은 표준 기저 벡터를 사용하는 것입니다. 이는 벡터 공간의 기본적인 속성들을 대부분 보존하기 때문입니다.
다른 경우에는, 특히 좀 더 복잡한 벡터 공간에서는 기저 벡터를 선택하는 것이 더 복잡해질 수 있습니다. 이 경우, 일반적으로 벡터 공간의 선형 관계들을 고려하여 기저 벡터를 선택합니다. 예를 들어, 어떤 벡터 공간에서 일부 벡터들이 다른 벡터들의 선형 조합으로 표현될 수 있다면, 이들 중 하나 이상은 기저 벡터가 될 수 있습니다.
기저 벡터는 왜 중요한가요?
기저 벡터는 선형 대수학에서 매우 중요한 역할을 합니다. 벡터 공간에서 다른 모든 벡터는 기저 벡터의 선형 조합으로 표현될 수 있기 때문입니다. 이는 벡터 공간 내의 모든 벡터가 기저 벡터에 대한 선형 방정식을 포함하고 있다는 것을 의미합니다. 이런 관찰을 통해, 우리는 기저 벡터가 어떤 조합으로든 모든 벡터를 표현할 수 있음을 알 수 있습니다.
기저 벡터를 이용하면, 벡터 공간에 대한 더 깊은 이해를 얻을 수 있습니다. 벡터 공간 내의 모든 벡터를 기저 벡터로 표현하면, 벡터 공간의 연산과 성질들을 기저 벡터들 간의 연산과 성질로 분해할 수 있습니다.
또한 기저 벡터는 좌표계를 수립하는 데에도 중요한 역할을 합니다. 예를 들어, x-y 평면에서 (1,0)과 (0,1)은 표준 기저 벡터입니다. 이들을 이용하여 어떤 다른 벡터를 표현할 때, 선분 (1,0)과 (0,1)으로부터 추출한 좌표를 이용하여 그 벡터를 표현할 수 있습니다.
FAQs
Q. 기저 벡터는 무엇인가요?
A. 기저 벡터는 벡터 공간의 기초를 이루는 선형 독립적인 벡터들을 말합니다.
Q. 기저 벡터는 어떻게 선택되나요?
A. 기저 벡터를 선택하는 방법에는 여러 가지가 있습니다. 일반적으로 가장 간단한 선택은 표준 기저 벡터를 사용하는 것입니다.
Q. 기저 벡터는 왜 중요한가요?
A. 기저 벡터는 선형 대수학에서 매우 중요한 역할을 합니다. 벡터 공간에서 다른 모든 벡터는 기저 벡터의 선형 조합으로 표현될 수 있기 때문입니다.
기저 판별
In simpler terms, 기저 판별 is used to determine whether a given set of vectors in a vector space can be used as a basis or not. A basis is a set of vectors that can be used to create any other vector in that space through linear combinations.
The concept of bases and 기저 판별 is essential in many fields, including computer graphics, engineering, and physics, where it is used to solve problems related to linear algebra.
What is the Significance of 기저 판별?
In mathematics, vectors are mathematical objects that are used to represent quantities that have both magnitude and direction. In other words, vectors are used to represent physical quantities such as velocities, forces, and displacement.
Vector spaces are mathematical structures that consist of a set of vectors and a set of operations, namely addition and multiplication by scalars. These operations satisfy certain axioms that help define the properties of vector spaces.
For example, the set of all two-dimensional vectors forms a vector space known as R^2. Similarly, the set of all three-dimensional vectors forms a vector space known as R^3.
A basis is a set of vectors in a vector space that are linearly independent and can be used to create any other vector in that space through linear combinations. In other words, any vector in that space can be expressed as a unique linear combination of the basis vectors.
For example, in R^2, a standard basis is {(1,0), (0,1)}. Any vector in R^2 can be expressed as a linear combination of these two vectors. Similarly, in R^3, a standard basis is {(1,0,0), (0,1,0), (0,0,1)}.
기저 판별 is used to determine whether a given set of vectors in a vector space can be used as a basis or not. If the set of vectors is linearly independent, then it can be used as a basis. However, if the set of vectors is linearly dependent, then it cannot be used as a basis.
Linear independence refers to the property of a set of vectors, where no vector in the set can be expressed as a linear combination of the other vectors in the set. In other words, the vectors are independent of each other.
Linear dependence refers to the property of a set of vectors, where one or more vectors in the set can be expressed as a linear combination of the other vectors in the set. In other words, the vectors are dependent on each other.
기저 판별 is used to identify whether a set of vectors is linearly independent or linearly dependent. If the set of vectors is linearly independent, then it can be used as a basis to create any other vector in that space through linear combinations. On the other hand, if the set of vectors is linearly dependent, then it cannot be used as a basis.
Applications of 기저 판별 in Different Fields
기저 판별 is used in various fields, including computer graphics, engineering, and physics, where it is used to solve problems related to linear algebra.
In computer graphics, vector spaces are used to represent geometric objects such as points, lines, and surfaces. 기저 판별 is used to determine whether a set of vectors forms a basis that can be used to create any other vector in that space through linear combinations.
In engineering, 기저 판별 is used to determine whether a set of vectors forms a basis that can be used to describe the behavior of a system. For example, in control systems, a set of basis vectors can be used to describe the behavior of a dynamic system.
In physics, vector spaces are used to represent physical quantities such as forces, velocities, and displacements. 기저 판별 is used to determine whether a set of vectors forms a basis that can be used to describe the physical behavior of a system.
FAQs
1. What is a basis in mathematics?
A basis is a set of vectors in a vector space that are linearly independent and can be used to create any other vector in that space through linear combinations.
2. What is linear independence?
Linear independence refers to the property of a set of vectors, where no vector in the set can be expressed as a linear combination of the other vectors in the set.
3. What is linear dependence?
Linear dependence refers to the property of a set of vectors, where one or more vectors in the set can be expressed as a linear combination of the other vectors in the set.
4. What is the significance of 기저 판별?
기저 판별 is used to determine whether a given set of vectors in a vector space can be used as a basis or not.
5. What are some fields where 기저 판별 is used?
기저 판별 is used in various fields, including computer graphics, engineering, and physics, where it is used to solve problems related to linear algebra.
Conclusion
In conclusion, 기저 판별 or “Base Discrimination” is a concept in Korean that is widely used in mathematics. It is used to identify a set of vectors in a given vector space that can be used as a basis or not. The concept of bases is essential in many fields, including computer graphics, engineering, and physics, where it is used to solve problems related to linear algebra. The ability to identify a set of vectors that can form a basis is a crucial tool that helps us to model and solve problems in various fields.
주제와 관련된 이미지 기저함수

기저함수 주제와 관련된 이미지 26개를 찾았습니다.

![Linear Algebra] Lecture 26-(2) 정규직교기저와 푸리에 급수 그리고 오일러 공식(Orthonormal basis, Fourier series and Euler's formula) :: Learn Again! 러너게인 Linear Algebra] Lecture 26-(2) 정규직교기저와 푸리에 급수 그리고 오일러 공식(Orthonormal Basis, Fourier Series And Euler'S Formula) :: Learn Again! 러너게인](https://t1.daumcdn.net/cfile/tistory/9985EB485A5036B60B)
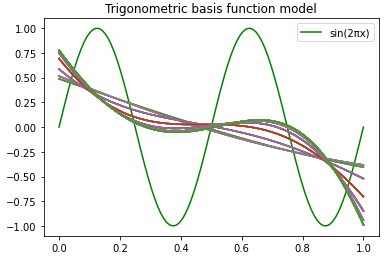
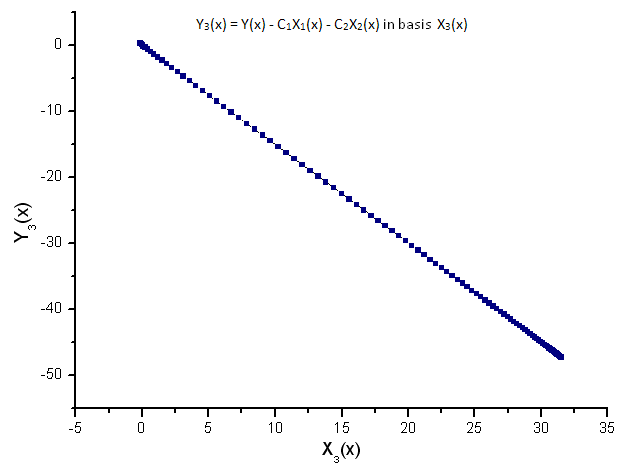
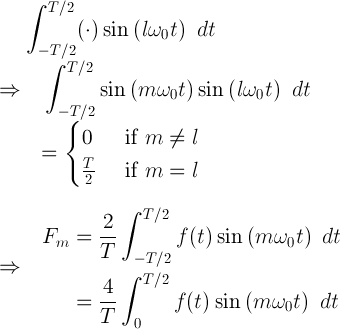


Article link: 기저함수.
주제에 대해 자세히 알아보기 기저함수.
- 6.2 기저함수 모형과 과최적화 – 데이터 사이언스 스쿨
- 기저 함수 – 위키백과, 우리 모두의 백과사전
- # 머신러닝 – Basis fuction (기저함수) : 네이버 블로그
- 기저 함수 – Wikiwand
- 기저 (Basis) – [정보통신기술용어해설]
- 기저 함수, 기저 벡터… 도대체 무엇을 말하는 건가요? – GpgStudy
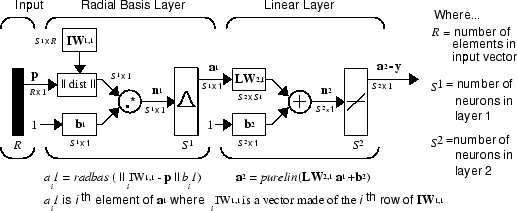
- 방사형 기저함수 – IBM
- 베이즈 데이터 분석(제3판) 5부: 제19장~제23장
더보기: https://shinbroadband.com/category/woki blog
