기어 잇수 공식
기어의 개념과 기어 비율
기어는 원래 회전 운동을 전달하고 변화시키는 기계 부품으로, 크기와 모양은 다양하다. 기어는 기어 비율에 따라 회전수를 변화시키기 때문에, 원 운동을 다른 회전 운동으로 변형하는 주요한 역할을 한다.
기어 비율은 입출력 회전수의 비율을 의미한다. 비율이 1인 경우, 입출력 회전수가 같고, 비율이 2인 경우, 입출력 회전수가 2배 높아진다. 따라서 기어 비율은 입력과 출력 사이의 회전수 변환을 수행하기 위한 중요한 매개체이다.
기어의 종류와 특징
기어는 다양한 종류가 있으며, 주요한 종류에는 취성기어, 헬리컬 기어, 스파이럴 기어, 평면 기어 등이 있다.
취성기어는 간단한 구조로 제조가 쉬우며, 저렴한 가격으로 제작할 수 있다. 헬리컬 기어는 대형 기계에서 많이 사용되며, 회전 운동이 부드러운 특징을 가지고 있다. 스파이럴 기어는 매우 높은 부하를 지원할 수 있으며, 힘의 잘 전달되는 특성을 가진다. 평면 기어는 크기가 작아서 가볍고, 소음이 적어 대중적으로 사용되는 기어이다.
기어의 회전수, 회전 방향의 결정
기어는 회전 운동을 전달할 뿐만 아니라, 회전 방향도 결정한다. 왼쪽으로 회전하는 원 운동을 입력하면, 오른쪽으로 회전하는 기어 출력이 나오게 된다. 이때, 회전 방향의 결정은 간단한 공식으로 구할 수 있다.
회전 방향의 결정 공식은 다음과 같다.
1. 입력 기어의 이음계수와 출력 기어의 이음계수를 계산한다.
2. 이음계수가 같으면, 회전 방향은 동일하다.
3. 이음계수가 다르면, 회전 방향은 반대로 된다.
이처럼 회전 방향의 결정은 간단한 공식을 사용하여 빠르게 결정할 수 있다.
기어 잇수 공식의 역할과 필요성
기어 잇수 공식은 기계 공학 분야에서 가장 중요한 도구 중 하나이다. 기어는 회전 운동을 변환하고 전달하는데 사용되기 때문에, 기어 잇수 공식을 사용하여 필요한 회전수를 디자인하고, 최적의 작동 조건을 찾아내는 것이 매우 중요하다.
예를 들어, 주요 원동기의 구동 장치에서는, 적정한 입력 회전수와 출력 회전수를 가진 기어를 조합하여 작동하도록 구성해야한다. 이때, 기어 잇수 공식을 사용하여 최적의 기어 비율을 설정하여 엔진의 작동 효율을 극대화할 수 있다.
기어 잇수 공식의 공식 종류와 차이점
기어 잇수 공식은 여러 가지 종류가 있다. 대표적인 공식으로는 간단한 기어, 헬리컬 기어, 스파이럴 기어, 평면 기어 등이 있다. 이들 기어는 잇수 공식이 다르며, 각각의 특성에 따라 다른 용도로 사용된다.
간단한 기어는 회전 운동을 전달하는 기본적인 기어로, 회전 운동을 1:1로 전달한다. 헬리컬 기어는 대형 기계에서 많이 사용되며, 회전 운동이 부드러운 특징을 가진다. 스파이럴 기어는 높은 부하를 지원할 수 있으며, 힘의 잘 전달되는 특성을 가진다. 평면기어는 크기가 작아서 가볍고, 소음이 적어 대중적으로 사용되는 기어이다.
이들 공식은 각각 다른 잇수 비율과 특성을 가지고 있기 때문에, 다양한 용도에 맞게 선택하여 사용해야 한다.
역학적 해석을 통한 기어 잇수 공식의 응용
역학 분야에서는, 기어 비율을 정확하게 계산하여 최적의 조건을 찾아내는 것이 매우 중요하다. 기어 잇수 공식을 사용하여 기어 비율을 계산하는 것은 매우 중요한 업무이며, 이를 통해 구성하는 기어 조합에 있어서 회전 운동의 전달과 전달되는 힘의 방향이 적절하게 이루어질 수 있게 된다.
스파이럴 기어와 기어 잇수 공식
스파이럴 기어는 회전 운동을 직선 운동으로 전달하는데 많이 사용된다. 이때, 스파이럴 기어의 잇수 공식이 중요한 역할을 한다.
스파이럴 기어의 잇수 공식에는 전체 잇수, 유효 잇수가 있다. 전체 잇수는 전체 기어 잇수를 나타내며, 유효 잇수는 효율적인 회전 운동을 위해 필요한 최소 치수 잇수를 나타낸다.
평면 기어와 기어 잇수 공식
평면 기어는 크기가 작아서 가볍고, 소음이 적어 대중적으로 사용되는 기어이다. 이때, 평면 기어의 잇수 공식은 간단한 구조로 공식화하기가 용이하므로 매우 중요하다.
헬리컬 기어와 기어 잇수 공식
헬리컬 기어는 대형 기계에서 많이 사용되며, 회전 운동이 부드러운 특징을 가진다. 이때, 헬리컬 기어의 잇수 공식은 수학적으로 복잡하지만, 생산성을 높이기 위해 컴퓨터 프로그램을 활용하여 공식화하기도 한다.
기어 잇수 공식의 실험과 적용 가능성
기어 잇수 공식은 실험이 중요하다. 기어의 작동 원리와 목적에 따라 최적의 기어 조합을 찾기 위해 다양한 실험과 자료 수집이 필요하다.
기어 모듈 규격, 기어 공식, 기어 모듈 단위, 기어 모듈이란, 헬리컬 기어 모듈, 스퍼기어 규격, 기어 압력각, 기어 계산기어 잇수 공식
기어 잇수 공식을 사용하여 기어비를 결정할 때, 기어 모듈 규격, 기어 공식, 기어 모듈 단위, 기어 모듈이란, 헬리컬 기어 모듈, 스퍼기어 규격, 기어 압력각, 기어 계산 등 다양한 요소를 고려해야 한다. 이들 요소를 잘 이해하고 고려하여 기어 잇수 공식을 적용하는 것이 필요하다.
FAQs
1. 기어 잇수 공식은 무엇인가요?
– 기어 잇수 공식은 기계 공학 분야에서 사용되는 중요한 개념 중 하나이며, 기어의 회전수와 회전 방향, 기어비 등을 결정하는데 사용된다.
2. 기어가 무엇인가요?
– 기어는 기계 작동에 있어서 매우 중요한 역할을 하며, 회전 운동을 주어진 한 회전 수에서 다른 회전 수로 전달하는데 사용된다.
3. 기어 비율이란 무엇인가요?
– 기어 비율은 입력 회전 수와 출력 회전 수의 비율을 의미한다. 기어 비율이 높을수록, 출력 회전 수는 입력 회전 수보다 더 높아진다.
4. 기어 잇수 공식의 종류는 무엇인가요?
– 기어 잇수 공식에는 간단한 기어, 헬리컬 기어, 스파이럴 기어, 평면 기어 등 다양한 종류가 있다.
5. 기어 잇수 공식은 언제 사용하나요?
– 기어 잇수 공식은 기계 작동 원리를 이해하고, 최적의 기어 조합을 찾기 위해 사용된다. 회전 운동과 전달되는 힘의 방향을 이해하는데 중요하며, 개발, 설계, 생산, 테스트 등 다양한 단계에서 필요하다.
6. 기어 모듈 단위는 무엇인가요?
– 기어 모듈 단위는 기어의 크기와 모양을 측정하는 단위이다. 기어 모듈은 Z/N으로 표시되며, Z=기어 이음계수, N=모듈 단위를 의미한다.
7. 스파이럴 기어와 기어 잇수 공식은 어떻게 관련되어 있나요?
– 스파이럴 기어는 회전 운동을 직선 운동으로 변화하는데 많이 사용되며, 스파이럴 기어의 잇수 공식이 중요한 역할을 한다. 잇수 공식이 다르므로, 각각의 스파이럴 기어에 맞게 최적의 기어 비율을 계산해야 한다.
사용자가 검색한 키워드: 기어 잇수 공식 기어 모듈 규격, 기어 공식, 기어 모듈 단위, 기어 모듈이란, 헬리컬 기어 모듈, 스퍼기어 규격, 기어 압력각, 기어 계산
Categories: Top 62 기어 잇수 공식
여기에서 자세히 보기: shinbroadband.com
기어 모듈 규격
기어 모듈 규격이란 무엇인가요?
기어 모듈 규격은 기어 모듈을 만들기 위해 필요한 가공 기술에 관한 규격입니다. 이 규격은 다양한 산업 분야에서 사용되며, 기어 모듈의 크기, 형태, 각도 등 다양한 사항들에 대한 표준화를 이루어줍니다. 이러한 표준화는 기어 모듈을 만드는 공장들에서 동일한 규격을 사용함으로써 생산성을 향상시키고, 기어 모듈이 사용되는 산업 분야들에서도 상호 호환성을 확보할 수 있게 됩니다.
기어 모듈 규격에는 어떤 종류가 있나요?
기어 모듈 규격에는 다양한 종류가 있습니다. 그 중에서도 대표적인 것들은 디네이션 모듈, 미터 모듈, 야드 모듈 등이 있습니다.
– 디네이션 모듈(DP: Diametral Pitch) : 이 모듈 규격은 기어의 직경과 이빨 당 톱니 수의 비율을 나타내는 것으로, 미국에서 주로 사용되는 규격입니다. 인치 단위로 표기됩니다.
– 미터 모듈(MP: Module Pitch) : 이 모듈 규격은 기어의 직경에 대해 톱니 당 모듈 수를 의미하며, 유럽에서 많이 사용되는 규격입니다. 메트릭 단위로 표기됩니다.
– 야드 모듈(SA: Systeme de Arbel) : 이 모듈 규격은 미터 모듈에 비해 생산성이 높은 규격입니다. 프랑스에서 주로 사용되며, 야드라는 단위로 표기됩니다.
기어 모듈 규격은 어떻게 선택되나요?
기어 모듈 규격은 기어의 사용 목적에 따라 선택됩니다. 기어 모듈은 다양한 산업 분야에서 사용되며, 그에 따라 다양한 규격이 존재합니다. 예를 들어, 자동차 등에서 사용되는 기어의 경우는 디네이션 모듈을 주로 사용하며, 기계 공작 기계에서 사용되는 기어의 경우는 미터 모듈을 주로 사용합니다. 따라서 기어 모듈을 사용하는 산업 분야와 사용 목적에 따라 해당하는 규격을 선택하면 됩니다.
기어 모듈을 제조하는 공장에서는 기어 모듈 규격을 어떻게 준수하나요?
기어 모듈을 제조하는 공장에서는 규격을 준수하기 위한 다양한 공정을 거칩니다. 예를 들어, 기어 모듈은 다양한 가공 기술을 사용하여 생산됩니다. 이렇게 생산된 기어 모듈은 규격에 맞게 기계부에 장착됩니다.
또한 기어 모듈은 특정한 조건에서 사용되므로, 내구성과 정밀도가 매우 높아야 합니다. 따라서 공장에서 생산된 기어 모듈은 다양한 검사 과정을 거쳐 최종 제품으로 출고됩니다. 이러한 과정들을 철저히 실시하여 규격을 준수할 수 있도록 노력하고 있습니다.
기어 모듈을 사용하는 산업 분야에서는 어떻게 규격을 확인하나요?
기어 모듈을 사용하는 산업 분야에서는 기어 모듈에 대한 규격을 확인하기 위한 다양한 방법들이 존재합니다. 예를 들어, 기전적인 방법으로는 기어 모듈의 외경, 기어모듈의 톱니 형태, 기어 모듈의 모듈 등을 측정하여 규격을 확인할 수 있습니다. 또한 기어 모듈의 제조업체에서는 생산된 제품에 대한 제품 인증서를 발급하며, 이를 이용하여 제품의 규격을 확인할 수 있습니다.
기어 모듈 규격을 준수하지 않으면 어떤 문제가 발생할까요?
기어 모듈 규격을 준수하지 않으면 생산성 저하, 제품의 안정성 저하, 제품의 정확도 저하 등 다양한 문제가 발생할 수 있습니다. 특히, 기어 모듈은 정밀한 가공 기술을 요구하므로, 규격을 준수하지 않으면 톱니의 간섭 문제 등이 발생할 수 있습니다. 이러한 문제들은 제품의 안정성을 저하시키며, 제품의 수명을 단축시킬 수 있습니다.
기어 모듈 규격을 준수하여 제품을 생산하면 어떤 장점이 있나요?
기어 모듈 규격을 준수하여 제품을 생산하면 생산성 향상, 제품의 정확도 향상, 자원 절약 등 다양한 장점이 있습니다. 특히, 기어 모듈 규격을 준수하면 제품의 생산성을 높일 수 있어 생산 라인에서의 효율성을 높일 수 있습니다. 이러한 효과는 수요량이 많은 제조 산업 분야에서 더욱 큰 효과를 보입니다.
FAQs
1. 기어 모듈 규격중 디네이션 모듈과 미터 모듈은 어떻게 구분되나요?
디네이션 모듈은 인치 단위로 표기되며, 기어의 직경과 이빨 당 톱니 수의 비율을 나타냅니다. 미터 모듈은 메트릭 단위로 표기되며, 기어의 직경에 대해 톱니 당 모듈 수를 의미합니다.
2. 단위가 다른 기어 모듈 규격을 혼용하여 사용해도 될까요?
단위가 다른 기어 모듈 규격을 혼용하여 사용하면 잠재적으로 문제가 발생할 수 있습니다. 따라서 사용하는 산업 분야와 목적에 따라 규격의 단위를 통일해야 합니다.
3. 기어 모듈 규격 준수 여부는 어떻게 확인할 수 있나요?
기어 모듈 규격 준수 여부는 다양한 방법들을 통해 확인할 수 있습니다. 가공된 기어 모듈에 대한 규격을 제공하는 인증서를 확인하거나, 실제 산업 현장에서 기어 모듈의 외경, 톱니 형태, 모듈 등을 측정하여 확인할 수 있습니다.
4. 기어 모듈 규격을 준수하지 않으면 어떤 문제가 발생할까요?
기어 모듈 규격을 준수하지 않으면 생산성 저하, 제품의 안정성 저하, 제품의 정확도 저하 등 다양한 문제가 발생할 수 있습니다. 특히, 기어 모듈은 정밀한 가공 기술을 요구하므로, 규격을 준수하지 않으면 톱니의 간섭 문제 등이 발생할 수 있습니다.
기어 공식
Basics of the GCF formula
The GCF formula is essentially an equation that finds the gear ratio between two gears in a train. This ratio, also known as the reduction ratio, determines how much the speed or torque will increase or decrease between the two gears. The GCF formula is derived from two main components – pitch circle diameter and number of teeth on the gear.
Pitch circle diameter is the imaginary circle that intersects the teeth of a gear. The diameter of this circle is crucial for calculating gear ratios as it is directly proportional to the distance that a gear will travel with one complete rotation. The pitch circle is the point where two gears in contact with each other can transmit power between them.
The number of teeth on a gear also plays a vital role in the GCF formula. The number of teeth determines the gear’s speed and torque, and it is inversely proportional to the pitch circle diameter. This means that as the number of teeth increases, the pitch circle diameter decreases. The gear ratio is derived by comparing the pitch circle diameter of the two gears.
The GCF formula can be expressed as:
GCF = D₁ / D₂ = N₂ / N₁
Here, D₁ and D₂ represent the pitch circle diameter of gear 1 and gear 2, respectively. N₁ and N₂ represent the number of teeth on gear 1 and gear 2, respectively. The gear ratio is represented by GCF, and it is a dimensionless quantity.
Applications of the GCF formula
The GCF formula has numerous applications in the mechanical engineering industry. It helps engineers design efficient gear trains that can transmit power smoothly and minimize energy loss. Some of the essential applications of the GCF formula are:
1. Designing gear trains for power transmission systems: The GCF formula is a vital tool for designing gear trains in various power transmission systems such as automobiles, airplanes, and industrial machines. The accurate gear ratios calculated using the GCF formula allows engineers to optimize the gear system’s efficiency, reliability, and longevity.
2. Calculating speed and torque in gear systems: The GCF formula can be used to calculate the speed and torque of the gear system by applying the gear ratio to the input power. This helps engineers determine the output power, which is essential for calculating the gear system’s efficiency.
3. Selecting appropriate gears: The GCF formula helps engineers select suitable gears for a particular application based on the required gear ratio. This ensures that the gear system can handle the required power and speed without failure or wear.
4. Analysis of gear performance: The GCF formula is also useful in analyzing the gear system’s performance by comparing expected gear ratios with actual gear ratios. This helps engineers identify any issues with the gear system and take corrective actions to improve system performance.
Advantages of the GCF formula
The GCF formula provides numerous advantages to gear system design and analysis. Some essential benefits of the GCF formula are:
1. Accurate gear ratios: The GCF formula provides a precise calculation of the gear ratio, ensuring that the gear system can provide the necessary power and speed for a specific application.
2. Optimized gear system efficiency: The GCF formula helps engineers design gear systems with optimized efficiency, reducing energy loss and heat generation.
3. Reduced risk of gear failure: The GCF formula allows engineers to select appropriate gears for a particular application, reducing the risk of gear failure due to overload or wear.
4. Simplified gear analysis: The GCF formula simplifies the analysis of gear performance and helps engineers identify and troubleshoot issues efficiently.
FAQs about the GCF formula
1. What is the importance of the pitch circle diameter in the GCF formula?
The pitch circle diameter is essential in the GCF formula as it determines the gear ratio between two gears. The distance each gear travels with one complete rotation is directly proportional to its pitch circle diameter. Thus, the pitch circle diameter determines the speed and torque of the gear and helps calculate the gear ratio.
2. What is the gear ratio, and how is it calculated using the GCF formula?
The gear ratio is the ratio of the angular velocity of the input gear to the angular velocity of the output gear. The gear ratio is calculated using the GCF formula by comparing the pitch circle diameter of the two gears. The gear ratio is represented by a dimensionless quantity, GCF, which is derived from the equation GCF = D₁ / D₂ = N₂ / N₁.
3. Can the GCF formula be used for any type of gear system?
The GCF formula can be used for any type of gear system, provided the system uses two gears in contact with each other. The GCF formula applies to all types of gears, including spur gears, bevel gears, helical gears, and worm gears.
4. What are some common applications of the GCF formula?
The GCF formula is commonly used in designing gear trains for power transmission systems such as automobiles, airplanes, and industrial machines. It is also used to calculate speed and torque in gear systems, select appropriate gears, and analyze gear system performance.
5. What are some advantages of using the GCF formula for gear system design?
The GCF formula provides numerous advantages to gear system design and analysis, including accurate gear ratios, optimized gear system efficiency, reduced risk of gear failure, and simplified gear analysis.
주제와 관련된 이미지 기어 잇수 공식
기어 잇수 공식 주제와 관련된 이미지 48개를 찾았습니다.
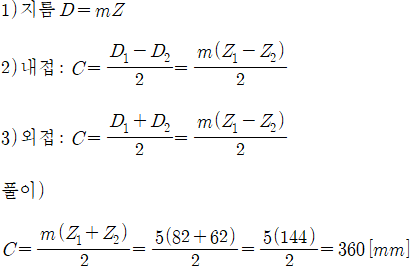

Article link: 기어 잇수 공식.
주제에 대해 자세히 알아보기 기어 잇수 공식.
- 기어의 모듈(Module)이란? 모듈 구하는 공식 – 네이버 블로그
- 기어의 모듈(Module)이란? 모듈 구하는 공식 – TechBox
- 기어의 모듈 구하는공식좀 가르쳐주세요 : 네이버 블로그
- 스퍼기어 명칭 및 작성 공식
- 【기계설계】 기어 단원 공식정리 – Engineering Help – 티스토리
- 전산응용기계제도기능사 – 기어의 계산식 [시험에 나오는것만 …
- 기어의 모듈(Module)이란? – 기어 이빨 크기의 단위
더보기: https://shinbroadband.com/category/woki blog
